
Alex Elzenaar
I (he/him) am currently in the School of Mathematics at Monash University supervised by Jessica Purcell. My research interests lie broadly in the intersection between classical geometry (in the style of Coxeter
and Thurston) and algebra. At the moment I focus particularly on constructing and studying representations of groups which arise from geometry.
One can view this as a direct generalisation of the study of wallpaper patterns: the objects being studied are more complicated but
have similarly rich connections to number theory and crystallography, and their study additionally draws from other areas including algebraic geometry, low-dimensional topology, knot theory,
and conformal geometry. I am also interested in visualisation of mathematical objects and their relation to art, and mathematical writing as a form of literature.
Email: alexander.elzenaar@monash.edu ▫ Curriculum Vitae ▫ Publications ▫ Theses and dissertations ▫ I am a top result on YouTube!
The knowledge of the adept embraces other fields, such as physiognosis, which deals with occult physics, the static, the dynamic, and
the kinematic, or astrology and esoteric biology, the study of the spirits of nature, hermetic zoology. I could add cosmognosis,
which studies the heavens from the astronomical, cosmological, physiological, and ontological points of view, and anthropognosis, which
studies human anatomy, and the sciences of divination, psychurgy, social astrology, hermetic history. Then there is qualitative
mathematics, arithmology...
– Umberto Eco, Foucalt's Pendulum, p.257. Vintage (2001).
Older quotes
Oppose hundreds of job cuts at Victoria University of Wellington (and thousands nationwide)

Where is your rage now? by Emma Maguire
Mathematical videos that I like: Coxeter on Escher's Circle Limit ▫ Not Knot ▫ Mathematics as metaphor ▫ Phyllotaxis ▫ How to write mathematics badly ▫ Hyperbolic VR ▫ The Riley slice ▫ Knots don't cancel ▫ Mixing ▫ Kaleidoscopes ▫ Hyperbolica by CodeParade ▫ Three-dimensional geometries ▫ Julia set capacitors ▫ Polyrhythms ▫ Quasicrystals ▫ Symmetry ▫ Cannon–Thurston maps
Other links and videos: some sculptures around Pōneke ▫ Hilma af Klint at the City Gallery in 2021-2022 ▫ Robin White: Making of That Vase ▫ Energy Work: Kathy Barry/Sarah Smuts-Kennedy ▫ "Rita" by Quentin Angus ▫ Patrick Pound at City Gallery Wellington ▫ Len Lye: A Colour Box, Colour Cry, Kaleidoscope ▫ A Painter's Journey: Rita Angus' Central Otago ▫ Solving Pale Fire ▫ The fiction of Borges ▫ Dan Olsen on creative inadequacy ▫ A good physics YouTube channel: String theory, Feynman ▫ Backlog of Mathematics Research Journals (2024) ▫ citations in the humanities
Look at these other people: Ari Markowitz, \( \mathbb{H}^3 \) group action visualiser and Bruhat-Tits tree visualiser ▫ David Groothuizen Dijkema ▫ Isabelle Steinmann ▫ Oliver Li
Publications and preprints
Full list with abstracts and detailed citations:
PDF
Preprints
- From disc patterns in the plane to character varieties of knot groups, 2025.
- arXiv:2503.13829 [math.GT].
- Changing topological type of compression bodies through cone manifolds, 2024.
- arXiv:2411.17940 [math.GT].
- On thin Heckoid and generalised triangle groups in \( \mathrm{PSL}(2,\mathbb{C}) \) (with Gaven Martin and Jeroen Schillewaert), 2024.
- arXiv:2409.04438 [math.GR].
- Bounding deformation spaces of 2-generator Kleinian groups (with Jianhua Gong, Gaven Martin, and Jeroen Schillewaert), 2024.
- arXiv:2405.15970 [math.CV].
Published
- Putatively optimal projective spherical designs with little apparent symmetry (with Shayne Waldron), 2025.
- Journal of Combinatorial Designs 33; dataset on Zenodo.
Preprint: arXiv:2405.19353 [math.CO], 2024.
- Concrete one complex dimensional moduli spaces of hyperbolic manifolds and orbifolds (with Gaven Martin and Jeroen Schillewaert), 2024.
- 2021–22 MATRIX Annals. MathSciNet: MR4807267.
Preprint: arXiv:2204.11422 [math.GT], 2022. Corrected preprint: PDF.
- The combinatorics of the Farey words and their traces (with Gaven Martin and Jeroen Schillewaert), 2024.
- Groups, Geometry, and Dynamics, published online first.
Preprint: arXiv:2204.08076 [math.GT], 2022.
- Approximations of the Riley slice (with Gaven Martin and Jeroen Schillewaert), 2023.
- Expositiones Mathematicae 41. MathSciNet: MR4557273.
Preprint: arXiv:2111.03230 [math.GT], 2021. Corrected preprint: PDF.
Miscellaneous unpublished expository writing
- The lake where they had hidden the reflections: Quasi-Fuchsian groups and their embeddings [This was a talk in a reading group.]
- Knot knotes
- Apocrypha and ephemera on the boundaries of moduli space [More detailed notes on deformations of geometrically finite Kleinian groups are under preparation.]
- Uniformisation, equivariance, and vanishing: three kinds of functions hanging around your Riemann surface
Selected talks
- Deformations of 3-orbifold holonomy groups and applications, 11 Dec. 2024 (slides)
- Uni. Auckland: Joint Meeting of the NZMS, AustMS and AMS, Early Career Showcase in Low-Dimensional Topology session.
- Limit sets of cone manifolds, 10 Dec. 2024 (poster)
- Uni. Auckland: Joint Meeting of the NZMS, AustMS and AMS, poster session.
- Combinatorial structures in trace polynomials of function groups, 28 Nov. 2024 (slides)
- ANU: 8th Australian Algebra Conference.
- Two-bridge knots, genus two surfaces, and discrete groups with two generators, 12 Nov. 2024 (slides)
- Uni. Melbourne: Geometry and topology in low dimensions: a conference celebrating the mathematics of Craig Hodgson.
- Is \( \mathrm{PSL}(2,\mathbb{Z}) \) discrete?, 24 Jul. 2024 (slides)
- Monash Uni.: Topology Seminar.
- The dynamic in the static: Manifolds, braids, and classical number theory, 10 May 2023 (slides)
- Uni. Leipzig: Regiomontanus PhD Seminar.
- What is a Kleinian group?, 21 Sep. 2022 (slides, recording)
- Online: Australian Postgraduate Algebra Colloquium.
- Pictures of hyperbolic spaces, 4 May 2022 (slides)
- TU Berlin: Discrete Mathematics and Geometry Seminar.
- The Farey polynomials, 6 Dec. 2021 (slides)
- Uni. Auckland: Waiheke Groups and Geometry Retreat.
- Approximating the Riley slice exterior, 2 Dec. 2021 (slides, recording)
- MATRIX Online: Workshop on Groups and Geometries.
- Real varieties of spherical designs, 1 Apr. 2021 (slides)
- Uni. Auckland: Algebra and Combinatorics Seminar.
Click for a list of other talks, lecture notes, and other ephemera.
- 7 May 2025: All arithmetic 2-bridge link groups in Topology Group Meeting, slides, notes.
- 12 March 2025: Rigid systems of poles and hinges in Topology Group Meeting, notes.
- Joint Meeting schedule
- November 2024: Variations on a theme of Wielenberg.
- July 2024: Reading group Hyperbolic Knot Theory, miscellaneous notes.
- 17, 18 July 2024: Guest lectures for MATHS 782 "Geometric Group Theory" (Uni. of Auckland), lecture notes for lecture 1b (surfaces), lecture notes for lecture 2a (conformal maps), miscellaneous problems, some books
- July-August 2023: Minicourse on knot theory and geometry (Uni. of Auckland), below.
- 16 March 2023: Connectedness of the Hilbert scheme in reading group of Javier and Angel, lecture notes.
- 17 to 20 January 2023: Apocrypha and ephemera on the boundaries of moduli space, a minicourse at the Uni. of Auckland (also 7 December 2022 at MPI), lecture notes.
- 10 October 2022: Uniformisation, equivariance, and vanishing: three kinds of functions hanging around your Riemann surface, at MPI, lecture notes.
- 3 August 2022: Reproducibility in Computer Algebra (MPI MIS), handouts for practical activity (event co-organised with Christiane Görgen and Lars Kastner).
- 15 July 2022: On the MathRepo page "Farey Polynomials", in the MathRepo: Data for and from your Research event (MPI MIS), slides.
- 24 May 2022: Projective varieties over \(\mathbb{C}\), in the Lorentzian polynomials day which I organised, slides.
- 27 April 2022: Strange circles: The Riley slice of quasi-Fuchsian space, in the Seminar on Nonlinear Algebra (MPI MIS), slides.
- 17 March 2022: Strange circles: The Riley slice of quasi-Fuchsian space, in Pedram Hekmati's seminar on moduli spaces (Uni. of Auckland), slides.
- 19 July 2021: The moulding of hyperbolic clay: Deformation spaces of Kleinian groups (Uni. of Auckland), presentation slides.
- 8 June 2021: Some properties of \(2 \times 2 \) matrices, in the UoA Dept. of Mathematics Student Research Conference, extended abstract, presentation slides.
[This talk was one of the four winners of the Best Talk award, along with the talks of Isabelle Steinmann, Chris Pirie, and David Groothuizen Dijkema.]
- Very rough lecture notes for the graduate seminar I taught on Kleinian groups in Semester 1, 2021: PDF 1,
PDF 2, further reading list, and post-mortem.
- October 2020: Tropical geometry and buildings (three lectures), notes.
- 23 July 2020: Toric varieties (Uni. of Auckland), presentation slides.
Deformation spaces of rank two Kleinian groups
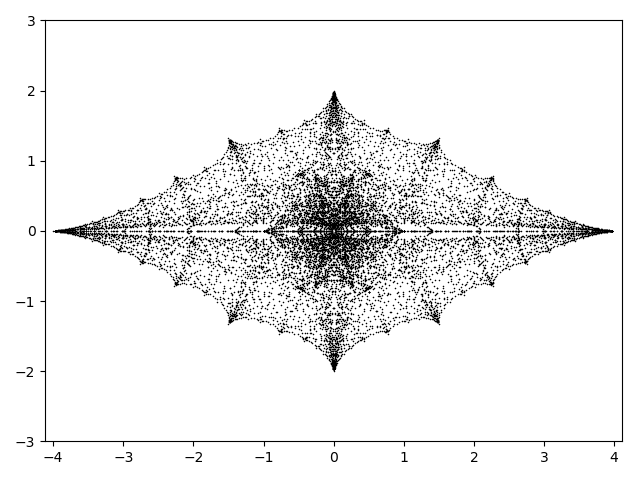
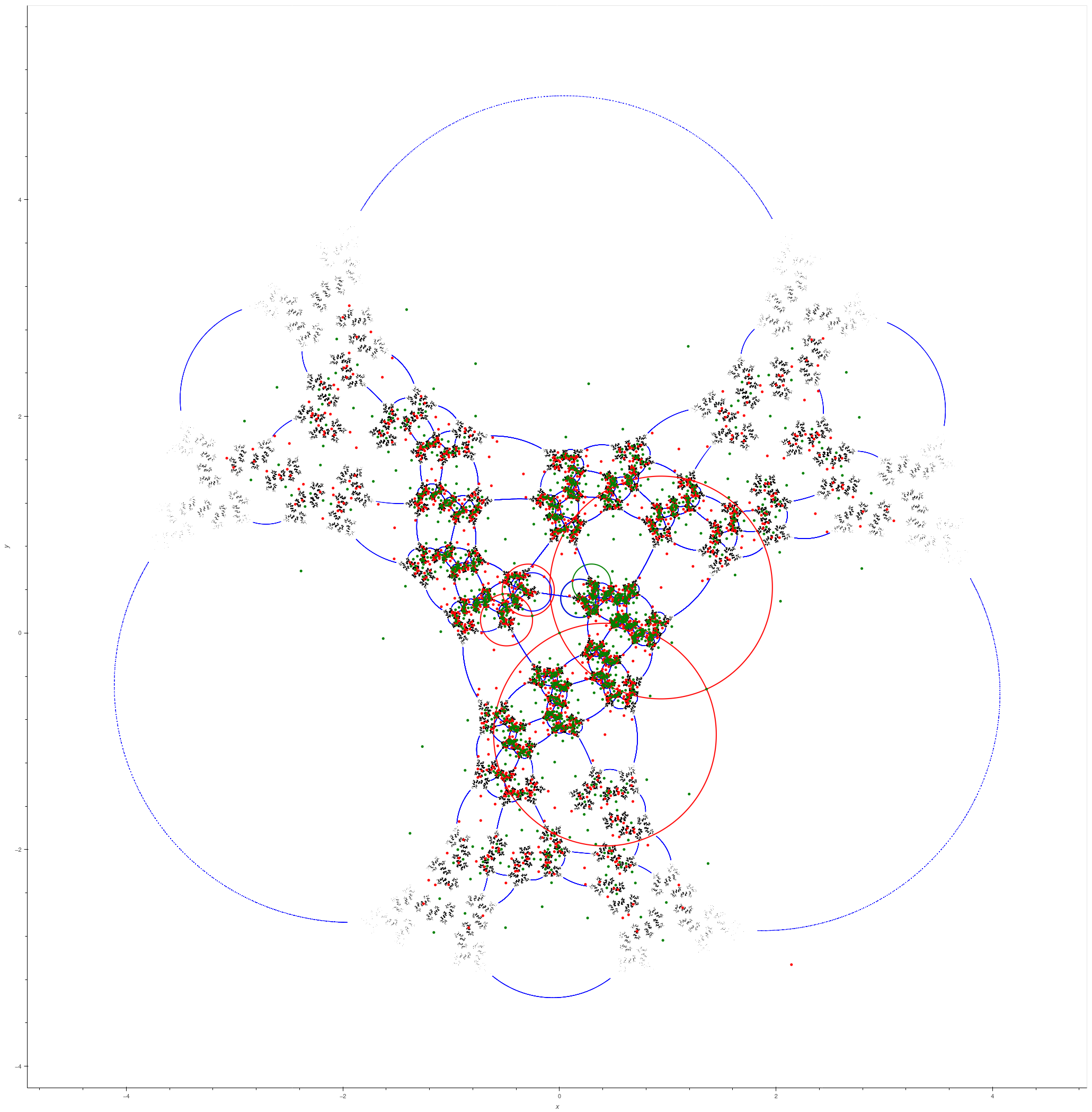
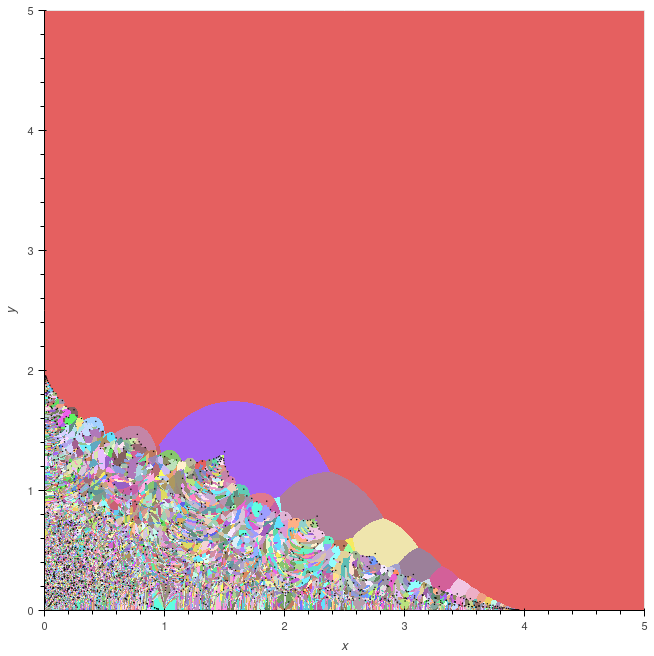
A rank two Kleinian group is a discrete subgroup of \( \mathrm{PSL}(2,\mathbb{C}) \) generated by two elements. If the group is non-elementary, then it is related in complicated and interesting
ways to hyperbolic 3-orbifolds that have boundary at infinity consisting of a genus two Riemann surface.
A graph curve is an algebraic curve consisting of a number of thrice-marked spheres, each marked point corresponding to a node (a transverse intersection of two components). Each graph curve
of genus two comes from a trivalent graph on two vertices and three edges. There are exactly two such graphs: the theta graph (each edge joins both nodes), and the handcuff graph (one edge
joins the nodes, and the others begin and end on the same node). Both of these graphs are homotopy retracts of the genus two handlebody. Therefore there are only two graph curves of genus two.
On the edge of the deformation space of 3-manifolds with genus two surface at infinity there lie manifolds with the same configuration of spheres at infinity: pairs of thrice-punctured spheres with
rank one cusps, with incidence graph a trivalent graph with two vertices and three edges (the incidence graph has vertices correspoding to topological components of the surface and edges corresponding
to nodes).
By Thurston's ending lamination theorem (proved for this special case by Minsky and Miyachi), on the boundary of the 3-manifold space you get a different limit for each choice of embedding of the
trivalent graph into the handlebody, and you can also take limits of such choices to get 'degenerate' orbifolds—the graphs might even be knotted! Conversely every boundary point arises in this way.
So there is a very complicated map from the space of these boundary groups (which is basically a Teichmüller space, up to a small quotient) to the space of graph curves (which has two points).
It turns out that this complicated map is basically reflecting the geometry of two-bridge links. Manifolds on the boundary that correspond to handcuff graphs arise from two-bridge links
with two components, and manifolds corresponding to theta graphs arise from two-bridge knots. The knots do not live inside the deformation spaces, but they lie on tendrils of discrete groups that creep
out beyond the moduli spaces.
The Riley slice is the space of Kleinian groups generated by two parabolic elements such that the quotient manifold is a Conway ball: a 3-ball with two arcs drilled out. Choosing a way of arranging
these arcs into a rational tangle is equivalent to picking a simple closed curve on the boundary sphere; suppose that this curve is represented by a hyperbolic element \( W_{p/q} \) with trace
\( \mathrm{tr}\, W_{p/q} < -2 \) in the holonomy group of the manifold (actually, you need to pick the correct component of the set of points where this word is hyperbolic, but this is immaterial for the
time being). The boundary of the deformation space can be reached by smoothly deforming \( W_{p/q} \) until it is parabolic (trace equals \( -2 \)).
Keep deforming \( W_{p/q} \) so that its trace decreases; the group is no longer discrete except sporadically, and these discrete groups correspond to replacing the parabolic arc with a cone arc. Eventually
you reach \( \mathrm{tr}\, W_{p/q} = 2\), and in fact \( W_{p/q} = 1 \). You have now reached the fundamental group of the \( p/q \) 2-bridge link. The arc (which has now vanished to become a solid part of the knot
complement) is an upper or lower unknotting tunnel for the knot; and the point on the boundary of the deformation space where this arc was parabolic corresponds to the manifold where both the knot and the
unknotting tunnel have been drilled out as parabolic arcs from \( \mathbb{S}^3 \).
If this sounds interesting:
- You might want to start with our expository article Concrete one complex dimensional moduli spaces of hyperbolic manifolds and orbifolds (joint work
with Gaven Martin and Jeroen Schillewaert) which we wrote to give historical and mathematical background: we aimed for this to be accessible to beginning graduate students with only
a little complex analysis and topology knowledge.
- (To appear) A comprehensive study of the groups generated by pairs of parabolic and elliptic elements, following work of Keen and Series and various others (joint with Martin and Schillewaert).
- Various authors have written papers in different areas. Some of the most important to us include The Riley slice of Schottky space (Keen
and Series), Parabolic representations of knot groups (Riley), Classification of non-free Kleinian groups generated by two parabolic transformations (Akiyoshi, Ohshika, Parker, Sakuma and Yoshida), Cusps in complex boundaries of one-dimensional Teichmüller space (Miyachi), and The tree of knot tunnels (Cho and McCullough).
- Work related to the discreteness problem: Approximations of the Riley slice (joint with Martin and Schillewaert); Bounding deformation spaces of 2-generator Kleinian groups (joint with Gong, Martin, and Schillewaert)
- A detailed abstract combinatorial study of certain polynomials which control the geometry of these groups: The combinatorics of Farey words and their traces (joint with Martin and Schillewaert), table to denominator 10.
- Applications to the enumeration of arithmetic groups: On Thin Heckoid and Generalised Triangle Groups in \( \mathrm{PSL}(2,\mathbb{C}) \) (joint with Martin and Schillewaert).
Cone manifolds and discrete geometry of indiscrete groups
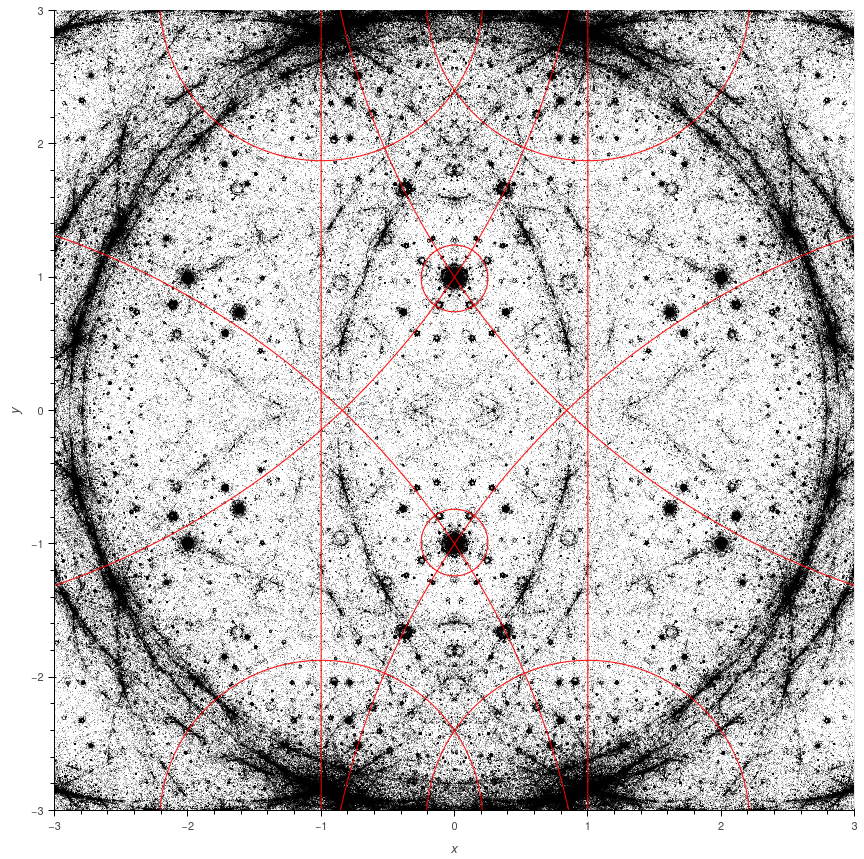
The abstract I submitted for my poster at the
joint meeting of the NZMS, AustMS and AMS is a good introduction to what I am thinking about currently:
Tilings of the plane or of more general 2D geometries are very classical and central mathematical objects. Their symmetry groups are discrete, and the quotients of the tilings by their symmetry groups are in the best case smooth surfaces and in the worst case surfaces with some bits that look like paper cones: take a disc of paper, cut a triangle out, and glue the resulting sides together. If you start with a tiling of the Euclidean or hyperbolic plane, the angles must be submultiples of \( \pi \). But if you're cutting triangles out of a piece of paper, there is no physical reason that you can't pick any angle you want: you still get a cone. Unwrap the corresponding surface, and you get a subset of the plane: it's just that the symmetry group is no longer discrete and if you try to make a tiling from it everything will overlap. Lots of abstract geometric group theory fails in this new setting, but if all you care about is taking a piece of paper, cutting angles out, and gluing a bunch of copies of the results together regardless, how much theory can you recover? We present some computer experiments and preliminary results in 3D: instead of gluing sheets of paper with corners, we glue imaginary blocks of hyperbolic space with corners.
More to come in 2025.
A zoo of Kleinian groups
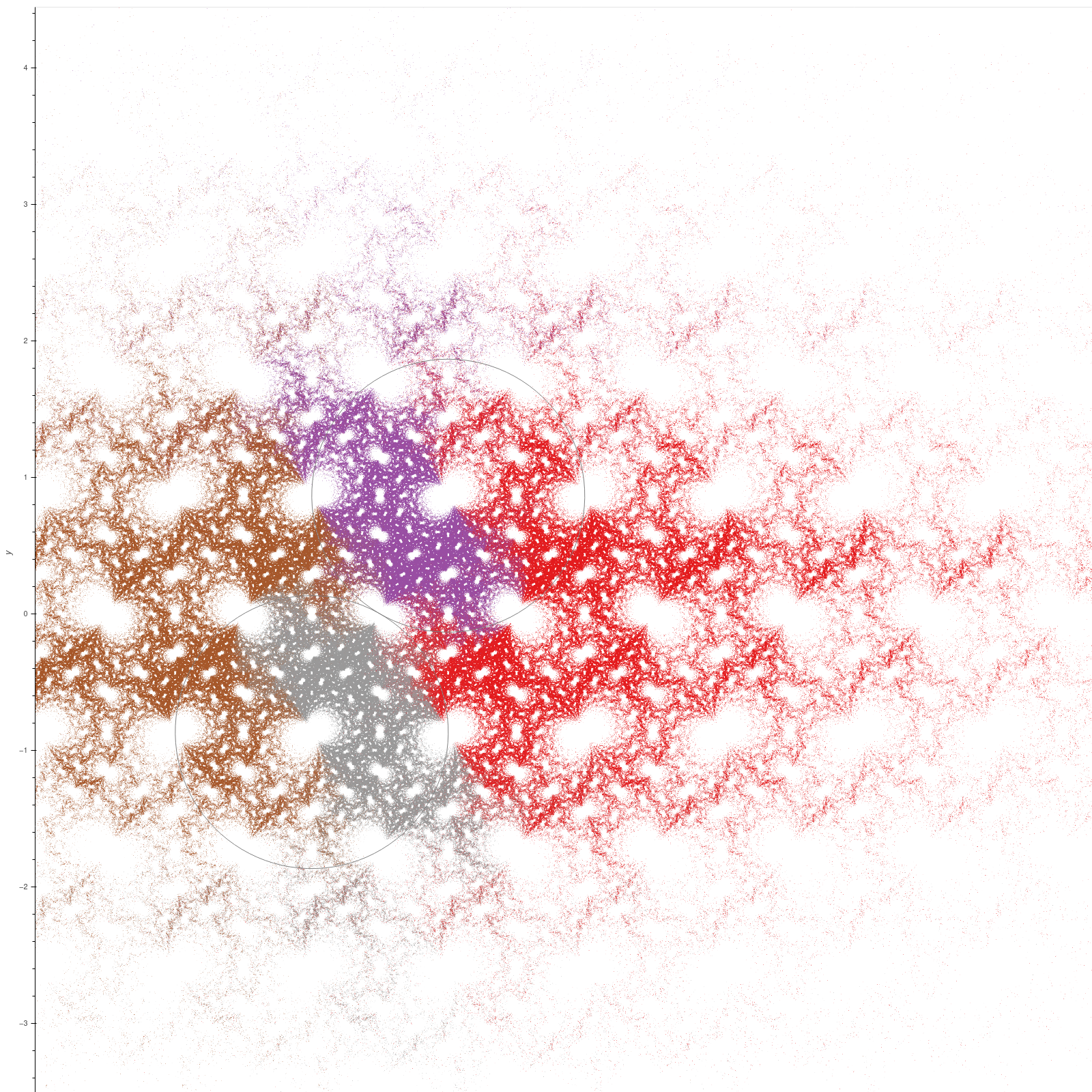
There are several useful 'zoos' of Kleinian groups with interesting properties; I collected several interesting groups and families of groups from a few sources,
and you can find their limit sets
on this page.
These images were produced using the Bella computational package for Kleinian groups. (Bella stood for Better Limit Set Drawer.)
A previous version of this package: Riley slice computational package (GitHub). With this earlier package I produced
some animations, and some more limit sets. Some more visually impressive animations can be
found on the website of Emily Dumas.
Minicourse on knot theory and geometry
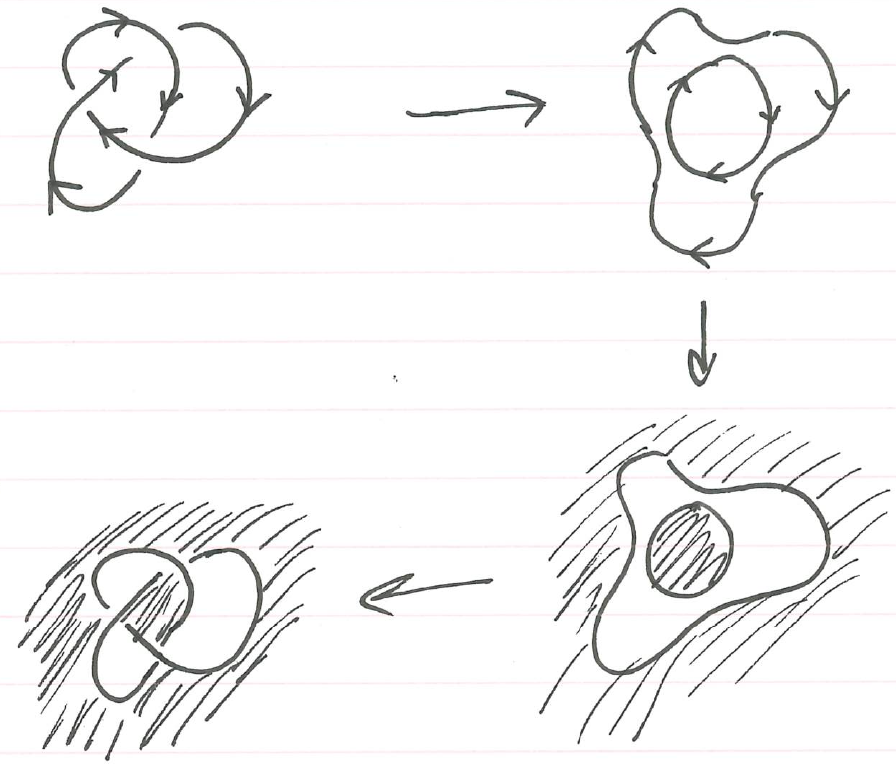
In July 2023 I organised a minicourse on knot theory at the University of Auckland, focusing on the representation theory of holonomy groups.
View the
abstract or download the latest version of the
notes.
Erratum: the Seifert surface of the figure eight knot drawn in the notes is not correct. A correct application of Seifert's algorithm and associated sketch may be found in L. Kauffman, On knots (Princeton), cited at that point in the notes.
There will be eight lectures over four weeks in 303.148 (for the first two weeks at least):
| Wed, 2pm | Fri, 2pm |
|---|
| Classical knot theory | 5 Jul: Basics | 7 Jul: Fundamental group |
|---|
| Geometric knot theory | 12 Jul: Knot complements | 14 Jul: Hyperbolic invariants |
|---|
| Braids | 19 Jul: Two-bridge knots | 21 Jul: Braids and mapping class groups |
|---|
| Knot polynomials | 26 Jul: Classical | 28 Jul: Quantum |
|---|
Josh Lehman gave the lecture on mapping class groups and Lavender Marshall gave the lecture on the Alexander polynomial.
Some useful links:
Lorentzian polynomials and algebraic geometry on matroids
If \( X \) is a sufficiently nice variety, the Chow group \( A^*(X) \) provides a homology theory on \( X \); in fact, it admits a ring structure coming from the intersection product. It turns out
that such a theory can be made to work on more general spaces, for example one can define a Chow ring for matroids; then the various Hodge-type results (Poincaré duality, the hard Lefschetz theorem,
and the Hodge-Riemann relations) carry over. Various nice polynomials can be defined with respect to this generalised Hodge theory and the associated cones of 'ample divisors' (which turn out
to be submodular functions); these are the
Lorentzian polynomials of Brändén and Huh.
A Day of Geometry and Lorentzian Polynomials
At the end of May 2022 there was a
seminar at the Institut Mittag-Leffler on the work of Branden, Huh, Katz, and various
other people on Lorentzian polynomials and the geometry of matroids; before this event on
Tuesday 24 May, I organised a very informal Zoom workshop on some of the geometric background
material.
Abstract.
Even if you do not know what Lorentzian polynomials are, you may have heard of Minkowski volume polynomials, the polynomials of the form \( \mathrm{vol}(x_1 K_1 + \cdots + x_n K_n) \)
where \( K_1,\ldots,K_n \) are convex bodies—and these are somehow the "canonical examples" of Lorentzian polynomials. The goal of the workshop is to give many different examples of Lorentzian
polynomials arising in geometry. The talks will be very informal, non-technical, and have many pictures.
The final schedule was as follows (all times are CET). Many of the speakers have kindly allowed me to share their slides and/or lecture notes.
- 9.30am—Matroids and chromatic polynomials (Tobias Boege, MPI MiS): Slides
- 10:15am—Varieties over C and embeddings into projective space via elliptic curves (Lukas Zobernig, The University of Auckland): Slides
- 11:00am—Hyperbolic polynomials (Hisha Nguyen, V.N. Karazin Kharkiv National University)
- Break (hopefully the morning talks are finished by 11:45, or 12 at the latest if we run over time).
- 1:30pm—Convex geometry & mixed volumes (Mara Belotti, TU Berlin): Slides
- 2:15pm—Projective varieties over \( \mathbb{C} \) (Alex Elzenaar, MPI MiS): Slides
Some background material
Spherical designs
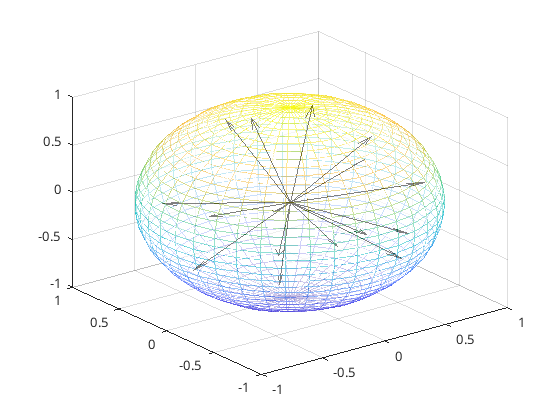
A spherical \((3,3)\)-design in \( \mathbb{R}^3 \) of 16 vectors.
Spherical \((t,t)\)-designs are arrangements of points on the sphere (possibly with weights) which are spaced 'far apart from each other': they are finite sets in \( \mathbb{R}^d \)
such that the integral over the sphere of each homogeneous polynomial of degree \(2t\) in \( d \) variables is equal to its average value on the set. There are generalisations
of this definition to subsets of \( \mathbb{C}^d \) and \( \mathbb{H}^d \) (the \(d\)-fold product of the Hamiltonian quaternion algebra, not hyperbolic \(d\)-space!).
Optimal designs and near-designs
Shayne Waldron and I have a paper in preparation:
Putatively optimal projective spherical designs with little apparent symmetry,
computing various spherical designs in order to find those of minimal order; a large set of designs and near-designs are archived on on Zenodo
at
DOI: 10.5281/zenodo.6443356. You can look at the code used to generate these
on
GitHub; it uses the
Manopt optimisation toolbox. This work was was funded in
part by a University of Auckland Summer Research Scholarship (2019-20). You can view the
final report for the scholarship.
Spherical designs and sums of squares
BSc(hons) dissertation and MSc thesis

I completed my BSc(Hons) dissertation in 2020 under the supervision of Dr. Jeroen Schillewaert.
My
Master of Science thesis was completed in 2021-22 in the Department of Mathematics at the
University of Auckland, under the supervision
of Dist. Prof. Gaven Martin (NZ Institute of Advanced Study, Massey University) and Dr. Jeroen Schillewaert.
For more information see
the section on deformation spaces above.





 The abstract I submitted for my poster at the joint meeting of the NZMS, AustMS and AMS is a good introduction to what I am thinking about currently:
The abstract I submitted for my poster at the joint meeting of the NZMS, AustMS and AMS is a good introduction to what I am thinking about currently:
 There are several useful 'zoos' of Kleinian groups with interesting properties; I collected several interesting groups and families of groups from a few sources,
and you can find their limit sets on this page.
There are several useful 'zoos' of Kleinian groups with interesting properties; I collected several interesting groups and families of groups from a few sources,
and you can find their limit sets on this page.
 In July 2023 I organised a minicourse on knot theory at the University of Auckland, focusing on the representation theory of holonomy groups.
View the abstract or download the latest version of the notes.
In July 2023 I organised a minicourse on knot theory at the University of Auckland, focusing on the representation theory of holonomy groups.
View the abstract or download the latest version of the notes.

 I completed my BSc(Hons) dissertation in 2020 under the supervision of Dr. Jeroen Schillewaert.
I completed my BSc(Hons) dissertation in 2020 under the supervision of Dr. Jeroen Schillewaert.